纳西妲生日快乐
太简单了不讲。
我们考虑对于每个 1 p v 操作算出它被执行了多少次,记作 sumi。设 muli 表示执行了 i 函数之后整个序列会乘上多少(也就是之前的函数会多执行多少次)。设我们正在处理第 i 次操作。对于 1 和 3 操作,它的 muli 肯定是 1。对于 2 操作,就有 muli=v。
我们对于每个 3 操作都从 i 向 ∀j∈[1,Ci],gj 建边。那么显然,它形成了一个 DAG。每个点的 mul 都是他们出到的点的 mul 的积。我们可以跑一遍拓扑排序,逆着拓扑序处理 mul。
如何处理 sum?我们发现 mulu 就是所有入到 u 的点的 sum 之和。我们可以顺着拓扑序处理。
那对于那些又有 1 又有 2 的 3 函数怎么搞呢?如图
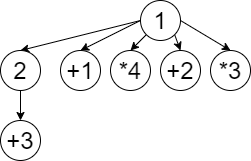
我们发现显然 +2 要多乘上一个 3,也就是说他要加上 sum1×3。对于 +1 显然要再多乘上一个 3×4=12。正好链式前向星是倒着的,所以我们维护一个 val 表示这个点要加上一个 val×sum。每处理完一个点,我们都要将 val 乘上它的 mul。
昨天晚上看题解给自己看破防了。
图片来自 AK_Dream 的博客↗,侵删。
分析分析还是分析。
做计数题之前一定要分析!
不自量力。
设我们正在求解 (0,0)→(x,y) 的答案,钦定 x≤y。
如果有 x=0,路径只有一条,长度为 2y(y+1)。
其次,如果有 y 是质数,一定有一条长为 x+y 的路径:(0,0)→(1,0)→(1,1)→(1,2)→⋯→(1,y)→(2,y)→⋯→(x,y)。
再其次,当 x 是质数时,设 k=⌊xy⌋。如果能在 (kx,y] 这个区间中找到一个质数,那么也可以是 x+y 的。
发现直接记搜就能过。还有我的 unordered_map 居然跑的和 map 一样快。
太脑电波了点。
设 x=cnt1+cnt0,y=cnt1−cnt0,那么就有两种情况:
- x:=x+1,y:=y+1:这个数取 1。
- x:=x+1,y:=y−1:这个数取 0。
问最后走到 (n+m,n−m) 且不经过 y=−1 方案数。
考虑总的方案数。那么就是从 n+m 里取 m 步往下走的方案数,显然是 (mn+m)。
考虑不合法的方案数。发现从 (0,0) 走到 y=−1 的方案数是 (0,−2) 走到 (n+m,n−m) 的方案数,为 (m−1n+m)。
所以最后的答案就是 (mn+m)−(m−1n+m)。
老早就看了这道题,一直没做出来。
我们枚举 i 表示第 i 种食材的数量 k>⌊2n⌋。转化一下发现 2k+n−j>n。发现 n−j 就是没选的点数量,选一个点 2k+n−j 就会 +2,不选就会 +1。所以我们枚举这行的每个点:aj,i。有转移:
⎩⎨⎧dpj,k←dpj−1,k×(sumj−aj,i)dpj,k+1←dpj,kdpj,k+2←dpj,k×aj,i不选当前列不选这个点选这个点
最后拿总的点减掉 ∑i=1m∑j=n+12ndpn,j 就是了。
后日谈
不自量力。
日记
周三 11月 20 2024 907 字 · 4 分钟

