斜率优化dp学习笔记

本人太弱，如果讲的不好，请见谅。

引入

斜率优化 dp，通常用于 dp 方程长成这个样子的题：

dp_{i} = \min\{dp_{j} + a_{i}b_{j} + c_{i} + d_{j}\}

因为有 $a_{i}b_{j}$ 这样的与 $i$ 和 $j$ 都有关的恶心项，所以不能用单调队列优化（虽然斜率优化有些时候也得用单调队列）。

例题

例题 1：P3195 [HNOI2008] 玩具装箱↗

既然叫斜率优化 dp，那么我们肯定得先把朴素的 dp 方程写出来。设 $dp_{i}$ 为前 $i$ 个玩具都塞进去了的最小代价，并维护前缀和 $sum_{i} = \sum\limits_{j = 1}^{i}C_{i} + 1$ ，那么有朴素的 dp 方程：

dp_{i} = \min\limits_{j = 0}^{i - 1}\{dp_{j} + (sum_{i} - sum_{j} - 1 - L)^{2}\}

方程很好理解，这里就不说了。那么现在我们考虑优化。为了方便，把 $L$ 提前加 $1$ ，然后把式子化简一下：

\begin{aligned} dp_{i} & = \min\{dp_{j} + (sum_{i} - sum_{j} - L)^{2}\} \\ & = \min\{dp_{j} + sum_{i}^{2} + (sum_{j} + L)^{2} - 2sum_{i}(sum_{j} + L)\} \\ & = sum_{i}^{2} + 2sum_{i}L + \min\{dp_{j} + (sum_{j} + L)^{2} - 2sum_{i}sum_{j}\} \\ \end{aligned}

化简的原则就是拆括号，然后把与内层循环无关的量扔出 $\min$ 。

考虑一次函数的斜截式 $y = kx + b$ ，移项变成 $b = y - kx$ ，原方程就该写作 $b_{i} = \min\{y - kx\}$ ，对于每一个 $i$ ，把在择优过程中不变的项（也就是只跟随 $i$ 变化的项，因为我们在讨论一个单独的 $i$ ，所以是“不变的项”）记在 $k$ 和 $b$ 里面，要变的（也就是会跟随 $j$ 变化的项）记在 $kx$ 和 $y$ 里面，具体一点，就是最小化的（也就是被扔出 $\min$ 的项和左边的 $dp_{i}$ ，还有一种描述是只跟 $i$ 有关的项）记作 $b$ ，和 $i,j$ 都有关的项记作 $kx$ ：只与 $i$ 有关的记作 $k$ ，只与 $j$ 有关的记作 $x$ 。剩下的只与 $j$ 有关的项记作 $y$ 。

看上面一大段文字会迷糊，不如来看看例子。在这道题的这个方程里，有：

\begin{aligned} x_{j} & = sum_{j} \\ k_{i} & = 2sum_{i} \\ y_{j} & = dp_{j} + (sum_{j} + L)^{2} \\ b_{i} & = dp_{i} - (sum_{i}^{2} + 2sum_{i}L) \end{aligned}

如果你看了还是迷糊，那么可以看看下面的例题里的式子，多看几遍，多推几遍就懂了。

那么我们看到一个东西： $b_{i} = dp_{i} - sum_{i}^{2}$ ，而 $sum_{i}^{2}$ 对于正在考虑的“固定”的 $i$ 是不变的，那么就可得：截距越小，决策更优（在有些题里是更大更优）。而 $k_{i}$ 也是不变的，那么就相当于：在平面直角坐标系里点了许多个点，第 $j$ 个点的坐标是 $(x_{j},y_{j})$ ，在编号属于 $[1,i)$ 的点里面找一个点 $j$ ，使得经过它的斜率为 $k_{i}$ 的直线截距最小。就像这样：

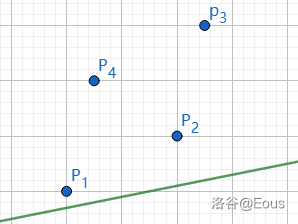
想象这条绿色的线在一直向上移动，它碰到的第一个点就是最优决策点。用盯真法，这里就是 $P_{1}$ 。但是程序不会盯真，所以我们还得想想怎么让程序也会找最优点。很显然，最优点一定在下凸壳（有些是上凸壳）上。于是我们可以用单调栈维护一个凸壳。但是凸壳有了，那凸壳上还有那么多点啊，到底是哪一个呢？

在这幅图里，很显然是最低点 $P_{1}$ ，那会不会有其他的情况呢，比如我们把这条线的斜率加大一点：

那现在就不是简单的最低点了，而是 $P_{2}$ 。但是，我们发现， $P_{1}$ 之所以不是最优解，是因为 $P_{1}P_{2}$ 这条线的斜率没有绿线大，导致 $P_{2}$ 先遇到绿线， $P_{1}$ 和前面的点（如果有的话）就都不会是最优决策点了。于是，我们可以把单调栈换成单调队列，然后在队尾，如果这个点与下一个点的连线比当前斜率 $k_{i}$ 要小（有些题是大），那么就把他扔出去，扔完之后的队尾就是最优决策点啦。因为每个点至多进出队列一次，所以时间复杂度为 $\mathcal{O}(n)$ 。

当然，还有一种做法，就是继续用单调栈，因为我们维护的是一个凸壳，所以斜率是具有单调性的，我们可以在单调栈上二分出第一个斜率大于等于当前斜率 $k_{i}$ 的第一个点就是最优决策点，时间复杂度 $\mathcal{O}(n \log n)$ ，没有单调队列做法优。

放一下代码：

1
#include<bits/extc++.h>
2
#define sq(x) ((x) * (x))
3
#define int long long
4
typedef long double ld;
5
using namespace std;
6
const int maxn = 5e4 + 5;
7
int n,l;
8
int c[maxn],sum[maxn],dp[maxn];
9
int q[maxn],head,tail;
10
ld x(int i){return sum[i];}//上文里的x[i]
11
ld y(int i){return dp[i] + sq(sum[i] + l);}//y[i]
12
ld k(int i){return (ld)2 * sum[i];}//k[i]
13
ld slope(int i,int j){return (y(j) - y(i)) / (x(j) - x(i));}
14
signed main()
15
{
16
    scanf("%lld%lld",&n,&l);
17
    l++;
18
    for (int i = 1; i <= n; i++)
19
    {
20
        scanf("%lld",c + i);
21
        sum[i] = sum[i - 1] + c[i] + 1;
22
    }
23
    head = 1,tail = 0;
24
    q[++tail] = 0;
25
    for (int i = 1; i <= n; i++)
26
    {
27
        while (head < tail && slope(q[head],q[head + 1]) <= k(i))
28
            head++;//将与下一个点的连线斜率小于等于当前k[i]的扔出去
29
        dp[i] = dp[q[head]] + sq(sum[i] - sum[q[head]] - l);
30
        while (head < tail && slope(q[tail - 1],q[tail]) >= slope(q[tail - 1],i))
31
            tail--;//维护凸壳
32
        q[++tail] = i;//压进队列
33
    }
34
    printf("%lld",dp[n]);
35
    return 0;
36
}

你肯定注意到了“有些题”和这个题不一样，至于为什么不一样呢？因为有些题的 $k_{i}$ 是单减的，所以是上凸壳，有些甚至没有单调性，那么我们就要用平衡树或者李超线段树来维护了。单调队列和单调栈只能用于维护横坐标和斜率都单调的方程。

例题 2：P4655 [CEOI2017] Building Bridges↗

这道题的斜率和横坐标就不单调了。

依旧是先列出朴素的方程：

dp_{i} = \min\{dp_{j} + w_{i - 1} - w_{j} + (h_{i} - h_{j})^{2}\}

其中 $w$ 是预处理好的前缀和。

接下来我们把它化简，并写出 $l,b,x,y$ ：

\begin{aligned} dp_{i} & = \min\{dp_{j} + w_{i - 1} - w_{j} + h_{i}^{2} + h_{j}^{2} - 2h_{i}h_{j} \} \\ & = w_{i - 1} + h_{i}^{2} + \min\{dp_{j} - w_{j} + h_{j}^{2} - 2h_{i}h_{j} \} \end{aligned}

写出 $l,b,x,y$ ：

\begin{aligned} k_{i} & = 2h_{i} \\ x_{j} & = h_{j} \\ b_{i} & = dp_{i} - w_{i - 1} - h_{i}^{2} \\ y_{j} & = dp_{j} - w_{j} + h_{j}^{2} \end{aligned}

但是我们发现： $x$ 和 $k$ 现在都不单调了，所以单调栈和单调队列立即发生爆炸。这时，我们就得请出李超线段树↗了。

板子这里就不说了。如果用李超线段树的话， $l,x,b,y$ 略有不同：

\begin{aligned} k_{j} & = -2h_{j} \\ x_{i} & = h_{i} \\ b_{j} & = dp_{j} - w_{j} + h_{j}^{2} \\ y_{i} & = dp_{i} - w_{i - 1} - h_{i}^{2} \end{aligned}

具体来说，就是把方程从 $b = y - kx$ 变成 $y = kx + b$ ，经过移项得到 $dp_{i} = kx + b + \text{something}$ 。这里的 $\text{something}$ 通常是固定的，所以我们可得 $kx + b$ 最小的是最优决策。那么我们就可以用李超线段树维护线段，查询横坐标为 $x_{i}$ 时最小的纵坐标。

放一下代码：

1
#include<bits/extc++.h>
2
#define int long long
3
#define sq(x) ((x) * (x))
4
#define inf 0x3f3f3f3f3f3f3f3f
5
using namespace std;
6
const int maxn = 1e5 + 5;
7
int n,cnt,rt;
8
int h[maxn],w[maxn],dp[maxn];
9
int k(int j){return -2 * h[j];}
10
int x(int i){return h[i];}
11
int b(int j){return dp[j] - w[j] + sq(h[j]);}
12
struct line
13
{
14
    int l,b;
15
    line(int k = 0,int b = 0):k(k),b(b){};
16
    int f(int x){return k * x + b;}
17
};
18
struct Nahida
19
{
20
    int ls,rs;
21
    line ln;
22
    bool fl;
23
}tree[maxn << 2];
24
void upd(line ln,int l,int r,int &rt)
25
{
26
    if (!rt)
27
        rt = ++cnt;
28
    int lpos = tree[rt].ln.f(l),rpos = tree[rt].ln.f(r);
29
    int lque = ln.f(l),rque = ln.f(r);
30
    if (!tree[rt].fl)
31
    {
32
        tree[rt].ln = ln;
33
        tree[rt].fl = 1;
34
        return;
35
    }
36
    else if (lque <= lpos && rque <= rpos)
37
        tree[rt].ln = ln;
38
    else if (lque < lpos || rque < rpos)
39
    {
40
        int mid = (l + r) >> 1;
41
        if (ln.f(mid) < tree[rt].ln.f(mid))
42
            swap(ln,tree[rt].ln);
43
        if (ln.f(l) < tree[rt].ln.f(l))
44
            upd(ln,l,mid,tree[rt].ls);
45
        else
46
            upd(ln,mid + 1,r,tree[rt].rs);
47
    }
48
}
49
int que(int pos,int l,int r,int rt)
50
{
51
    if (!rt)
52
        return inf;
53
    int ret = tree[rt].ln.f(pos);
54
    if (l == r)
55
        return ret;
56
    int mid = (l + r) >> 1;
57
    int tmp;
58
    if (pos <= mid)
59
        tmp = que(pos,l,mid,tree[rt].ls);
60
    else
61
        tmp = que(pos,mid + 1,r,tree[rt].rs);
62
    ret = min(ret,tmp);
63
    return ret;
64
}
65
signed main()
66
{
67
    scanf("%lld",&n);
68
    for (int i = 1; i <= n; i++)
69
        scanf("%lld",h + i);
70
    for (int i = 1; i <= n; i++)
71
    {
72
        scanf("%lld",w + i);
73
        w[i] += w[i - 1];
74
    }
75
    upd(line(k(1),b(1)),0,2e6,rt);//初始状态为dp[1]
76
    for (int i = 2; i <= n; i++)
77
    {
78
        dp[i] = que(x(i),0,2e6,rt) + w[i - 1] + sq(h[i]);//查询最小纵坐标
79
        upd(line(k(i),b(i)),0,2e6,rt);//加入线段树
80
    }
81
    printf("%lld",dp[n]);
82
    return 0;
83
}

例题 3：P4072 [SDOI2016] 征途↗

这题比较特殊，他的 dp 方程是二维的。我们还是先把朴素的方程写出来。设 $dp_{i,j}$ 表示到第 $i$ 走完 $i$ 条路用了 $j$ 天的最小方差。那么有：

dp_{i,j} = \min\{dp_{l,j - 1} + \text{这段的贡献} \}

那么问题就在于如何求贡献，我们先把方差的式子列出来：

v = \frac{\sum\limits_{i = 1}^{m}(len_{i} - \frac{sum}{m})^{2}}{m}

其中 $len_{i}$ 表示第 $i$ 天走的距离， $sum$ 表示到目的地的总距离。

现在按照题意，把 $v$ 乘上一个 $m^{2}$ ：

\begin{aligned} v \times m^{2} & = \frac{\sum\limits_{i = 1}^{m}(len_{i} - \frac{sum}{m})^{2}}{m} \times m^{2} \\ & = m \times \sum\limits_{i = 1}^{m}(len_{i} - \frac{sum}{m})^{2} \\ & = m \times \sum\limits_{i = 1}^{m}(len_{i}^{2} + \frac{sum^{2}}{m^{2}} - 2 \times len_{i} \times \frac{sum}{m}) \\ & = \sum\limits_{i = 1}^{m}(m \times len_{i}^{2} + \frac{sum^{2}}{m} - 2 \times len_{i} \times sum) \\ & = sum^{2} + \sum\limits_{i = 1}^{m}(m \times len_{i}^{2} - 2 \times len_{i} \times sum) \end{aligned}

那现在我们就知道每一段的贡献是 $m \times len_{i}^{2} - 2m \times len_{i} \times sum$ 。如此，我们的答案就是 $dp_{n,m} + sum^{2}$ 。记录 $dis$ 为距离的前缀和，用 $dis$ 里的数替换 $len_{i}$ 和 $sum$ ，并把完整的 dp 方程写出来：

dp_{i,j} = \min\{dp_{l,j - 1} + m(dis_{i} - dis_{l})^{2} - 2 \times (dis_{i} - dis_{l}) \times dis_{n} \}

接下来，我们尝试将它化简：

\begin{aligned} dp_{i,j} & = \min\{dp_{l,j - 1} + m(dis_{i} - dis_{l})^{2} - 2 \times (dis_{i} - dis_{l}) \times dis_{n} \} \\ & = \min\{dp_{l,j - 1} + m(dis_{i}^{2} + dis_{l}^{2} - 2dis_{i}dis_{l}) - 2dis_{i}dis_{n} + 2dis_{l}dis_{n} \} \\ & = \min\{dp_{l,j - 1} + m \times dis_{i}^{2} + m \times dis_{l}^{2} - 2m \times dis_{i}dis_{l} - 2dis_{i}dis_{n} + 2dis_{l}dis_{n} \} \\ & = m \times dis_{i}^{2} - 2dis_{i}dis_{n} + \min\{dp_{l,j - 1} + m \times dis_{l}^{2} - 2m \times dis_{i}dis_{l} + 2dis_{l}dis_{n} \} \end{aligned}

并尝试写出单调队列形式的 $k,x,b,y$ ：

\begin{aligned} k & = 2m \times dis_{i} \\ x & = dis_{l} \\ b & = dp_{i,j} - (m \times dis_{i}^{2} - 2dis_{i}dis_{n}) \\ y & = dp_{l,j - 1} + m \times dis_{l}^{2} + 2dis_{l}dis_{n} \end{aligned}

我们发现他的斜率单调递增，可以用单调队列来维护。那具体怎么做呢？我们最外层枚举 $j$ ，对于每一个 $j$ 对应的那一层，我们单独用一个单调队列维护，每层转移开始时清空并重新扔一个新的起始状态进去。

为什么要每层都用一个单独的单调队列？

因为每一层都是独立的，相当于重新开始了一次 dp。

更多细节会在代码里说明：

1
#include<bits/extc++.h>
2
#define int long long
3
#define sq(x) ((x) * (x))
4
using namespace std;
5
typedef long double ld;
6
const int maxn = 3005;
7
int n,m;
8
int dis[maxn];
9
int dp[maxn][maxn];
10
int q[maxn],head,tail;
11

12
//上文里的三哥俩
13
int k(int i){return 2 * m * dis[i];}
14
int x(int k){return dis[k];}
15
int y(int k,int j){return dp[k][j - 1] + m * sq(dis[k]) + 2 * dis[k] * dis[n];}
16

17
ld slope(int i,int k,int j){return ((ld)y(k,j) - (ld)y(i,j)) / ((ld)x(k) - (ld)x(i));}
18
signed main()
19
{
20
    scanf("%lld%lld",&n,&m);
21
    for (int i = 1; i <= n; i++)
22
    {
23
        scanf("%lld",dis + i);
24
        dis[i] += dis[i - 1];
25
    }
26
    memset(dp,0x3f,sizeof dp);
27
    dp[0][0] = 0;
28
    for (int j = 1; j <= m; j++)
29
    {
30
        //重中之重
31
        head = tail = 1;
32
        q[1] = j - 1;
33
        //因为前 j - 1 天至多走 j - 1 条路，所以初始的就是 j - 1
34
        for (int i = j; i <= n; i++)
35
        {
36
            while (tail > head && slope(q[head],q[head + 1],j) < k(i))
37
                head++;//维护凸壳
38
            int k = q[head];//本来以为会和上面的k(i)冲突的，但是实际上没有
39
            dp[i][j] = dp[k][j - 1] + m * sq(dis[i] - dis[k]) - 2 * (dis[i] - dis[k]) * dis[n];
40
            while (tail > head && slope(q[tail - 1],q[tail],j) > slope(q[tail],i,j))
41
                tail--;//加入队列
42
            q[++tail] = i;
43
        }
44
    }
45
    printf("%lld",dp[n][m] + sq(dis[n]));//输出答案
46
    return 0;
47
}

例题 4：P5308 [COCI2018-2019#4] Akvizna↗

这题要用一个叫 wqs 二分的东西。

依然先写出来朴素的 dp 方程。设 $dp_{k,i}$ 表示在前 $k$ 轮总共干了 $i$ 个人，那么有转移：

dp_{k,i} = \max\{dp_{k - 1,j} + \frac{i - j}{n - j} \}

然后化简：

\begin{aligned} dp_{k,i} & = \max\{dp_{k - 1,j} + \frac{i - j}{n - j} \} \\ & = \max\{dp_{k - 1,j} + \frac{i}{n - j} - \frac{j}{n - j} \} \\ & = \max\{dp_{k - 1,j} - \frac{j}{n - j} + i \times \frac{1}{n - j} \} \end{aligned}

写出 $k,x,b,y$

\begin{aligned} k & = -i \\ x & = \frac{1}{n - j} \\ b & = dp_{k,i} \\ y & = dp_{k - 1,j} - \frac{j}{n - j} \end{aligned}

然后看到 $k$ 和 $x$ 都单调，兴致勃勃的开始斜率优化。蛋柿，我们发现优化完了还是有 $\mathcal{O}(nk)$ 的复杂度，立即发生爆炸。这时候，就得请我们的 wqs 二分登场了。

wqs 二分通常用于求解“正好取 $k$ 组”的问题，能用它求解的问题通常还有一个特点：如果没有正好取 $k$ 的要求可以变成一维 dp。我们看，这道题正好满足条件。但是，wqs 二分还有一个要求，就是：设 $\operatorname{f}(k)$ 为正好取 $k$ 组的最优解，那么 $\operatorname{f}$ 是 $k$ 的凸函数（上凸下凸都可以）。证明的话，打表就可以。我们把每一个横坐标为整数 $k$ ，纵坐标为 $\operatorname{f}(k)$ 的每一个点都画出来：

因为凸壳的斜率具有单调性，所以我们尝试二分斜率。用二分到的斜率 $p$ 去切这个凸壳：

这时的截距就是 $ans - p \times k$ （这里的 $k$ 是横坐标）。因为会有 $k$ 次转移，所以我们在转移的时候，每次减去斜率 $p$ ，最终就会得到 $k$ 时截距 $b$ ，也就对应 $ans$ 最大值。并计算转移次数（或者叫分了几段）。因为斜率越大，切点越高，横坐标也就越大，分的段数也就越多，所以我们在 check 里面打斜率优化 dp，如果转移次数（分的段数）大于 $k$ ，那么就说明斜率太小了（结合图片理解），反之就是斜率太大了。

看看代码也许更加懂一些？

1
#include<bits/extc++.h>
2
using namespace std;
3
typedef long double ld;
4
const int maxn = 1e5 + 5;
5
const ld eps = 1e-15;
6
int tot,n;//这里的 tot 是题目中的 k
7
int q[maxn],head,tail;
8
ld dp[maxn],g[maxn];
9
inline ld x(int i){return (ld)1 / ld(n - i);}
10
inline ld y(int i){return (ld)dp[i] - (ld)i / ld(n - i);}
11
inline ld k(int i){return (ld)-i;}
12
inline ld slope(int i,int j){return (y(j) - y(i)) / (x(j) - x(i));}
13
bool check(ld mid)
14
{
15
    q[head = tail = 1] = 0;
16
    for (int i = 1; i <= n; i++)//check 里的斜率优化
17
    {
18
        while (head < tail && slope(q[head],q[head + 1]) - k(i) > -eps)//维护凸壳
19
            head++;
20
        int j = q[head];
21
        dp[i] = dp[j] + ld(i - j) / ld(n - j) - mid;
22
        g[i] = g[j] + 1;//记录转移次数（分的段数）
23
        while (head < tail && slope(q[tail],i) - slope(q[tail - 1],q[tail]) > -eps)
24
            tail--;
25
        q[++tail] = i;
26
    }
27
    return g[n] >= tot;//如果分的段数大于k，那么就说明斜率太小了。
28
}
29
int main()
30
{
31
    scanf("%d%d",&n,&tot);
32
    ld l = 0,r = 2e6,mid;
33
    while (r - l > eps && (ld)clock() / (ld)CLOCKS_PER_SEC < 0.9)
34
    {
35
        mid = (l + r) / (ld)2;
36
        if (check(mid))
37
            l = mid + eps;//斜率太小就加
38
        else
39
            r = mid - eps;//太大就减
40
    }
41
    check(l);
42
    printf("%.9Lf",dp[n] + 1.0 * l * tot);
43
    return 0;
44
}

总结

先将 dp 方程化简，尝试写单调队列形式的 $b = y - kx$ ：只与 $i$ 有关的项是 $b$ ，只与 $j$ 有关的项是 $y$ ，与 $i,j$ 都有关的项，分成两半：只与 $i$ 有关是 $k$ ，只与 $j$ 有关的是 $x$ 。
判断单调性。如果 $k,x$ 有一个不是单调的，那么就不能用单调队列维护凸包，推荐使用李超线段树，因为李超线段树不用任何单调性，而平衡树和 cdq 分治都有单调性的要求，时间复杂度也就多一个 $\log n$ 。
如果使用单调队列，那么队首就是最优决策点，用方程转移即可。
如果使用李超线段树，那么需要将 $k$ 和 $x$ 交换， $b$ 和 $y$ 交换，变成 $y = kx + b$ ， $x$ 与 $i$ 有关， $b$ 与 $j$ 有关。转移时，用李超线段树查询 $i$ 对应的 $x$ 的纵坐标的最小（最大值），也就是查询 $x = x_{i}$ 这条线与哪条插入的线段的交点纵坐标最大，为多少。那么查出来的最小（大）纵坐标就对应最优的决策值（ $y = kx + b$ ），转移即可。

如果有不严谨的地方，欢迎指出。

Thanks for reading!